Quiz of the Week - Chemistry 221 Dimensional Analysis and Scientific Notation

A Quick Review of Dimensional Analysis

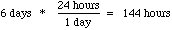
Dimensional analysis, also known as the factor-label method, is a problem solving technique using units (labels) and conversion factors. Units tell us the type of measurement being made; for example, "5.2 cm" has a unit (cm) which tells us the measurement to be made is length. Conversion factors (also known as "equalities") are fractions that relate two kinds of units; for example, "6.0 cm / s" tells us that for every 1 second that passes (time), 6.0 cm are covered (length). Notice that "6.0 cm s^-1" is the same as "6.0 cm / s" in unit notation.

Most problems ask a question whose answer is a number with its unit. Problems also give information that contains numbers with their units. Multiply the information by conversion factors so that all units cancel except the units needed in the answer. (A unit in the numerator may be canceled by placing the same unit in the denominator of the neighboring conversion factor. Conversely, a unit in the denominator may be canceled by placing the same unit in the numerator of the neighboring conversion factor.)

• Numbers and units are considered separately.
• Multiply by as many conversion factors as necessary.
• Common conversion factors may or may not be supplied with the problem.

Examples:

1. How many hours are in 6 days?

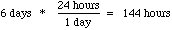
2. How many seconds are in 5 hours?

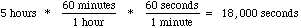
3. How many feet per second is 5 miles per hour?

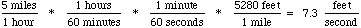
A common variation occurs when more than one piece of information is provided with the problem. In these cases, start with the information that contains the same type of units as the answer. (For example, if length units are needed in the numerator of the answer, use the information that contains length units and arrange it so that those length units are in the numerator.) Next, multiply by conversion factors so that unwanted units cancel.

Test Yourself:

1. How many gallons of milk does a family drink in 5 days if they drink 4 pints per day? Answer: 2.5 gallons

2. How many minutes will it take an automobile traveling 60 miles per hour to travel a distance of 400 miles?  Answer: 400 minutes

A Quick Review of Scientific Notation

Scientific Notation is used by scientists to express very large and very small numbers in a compact fashion.

To express a number in scientific notation, we rewrite the quantity as a number (between 1 and 10) times 10 raised to a power (exponent) that tells us how we moved the decimal point.

• Multiply the number by 10⁰ (10⁰ = 1)
• Move the decimal point to give a number between 1 and 10
• Every time we shift the decimal point to the left by one place, we increase the value of the exponent by one
• Every time we shift the decimal point to the right by one place, we reduce the value of the exponent by one

Example: Write 0.0000012 in scientific notation.

To express a number that is written in scientific notation as a non-exponential quantity:

• Move the decimal point the same number of places as the value of the exponent and eliminate the exponential part of the number.
• If the exponent is positive, we move the decimal to the right to the same number of places as the value of the exponent. The result should be a number greater than 1 unless the original number is negative.
• If the exponent is negative, we move the decimal to the left to the same number of places as the value of the exponent. The result should be a number less than 1 unless the original number is negative.

Example: Write 1.23 * 10⁶ in non-exponential form.

Example: Write 1.11 * 10^-5 in non-exponential form.

Chemistry 221 - Dimensional Analysis and Scientific Notation