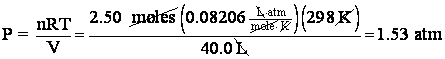4.        What is the temperature in degrees C of 5.78 L of a gas at 735 mmHg if it occupies 6.19 L at 18 degrees C and 925 mmHg?

It looks like this problem involves pressure, volume and temperature (P,V,T), so we need the general gas law (GGL): . We can rearrange it to solve for the final temperature, T₂:

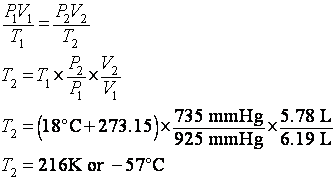
5.        How many moles of gas are present in a volume of 378 mL at 710 mmHg and -22 degrees C?

Here is a question that involves one of the BIG THREE (number of moles, a density or a number of molecules). In this case, it involves moles. So that means we have to use the IGL (ideal gas law) which relates pressure, volume, temperature and amount (number of moles). The IGL is, of course, PV = nRT where n is the number of moles and R is a proportionality constant called the Universal Gas Constant. R can have values of 0.08206 or 62.4 depending on the units you want for your answer or the units given in your problem. So... back to our problem. The question asks "How many moles..." so let's solve the IGL for n:

Temperature has to be converted to Kelvins: -22 degrees C+273.15 = 251K. We convert 378 mL to liters which is 0.378 L. We have a choice of how to treat the pressure. It's given in mmHg, so we could use the 62.4 value for R and use the mmHg pressure directly:

Notice how 378 mL was cleverly changed to 0.378L and degrees C was changed to Kelvins on-the-fly? We could also use the 0.08206 value for R by first converting the pressure from mmHg to atm. Since 1 atm = 760 mmHg (exactly), we can easily convert:

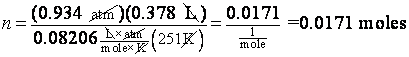
6.        What is the pressure of 6.54 mL of a gas sample at 57 degrees C if it occupies 9.75 mL at 21 degrees C and 1.64 atm?

This looks like another PVT problem. So we use . So we choose which set of PVT data has the subscripts 1 and which have the subscripts 2. P₁ = 1.64 atm, V₁ = 0.00975 L, T₁ = (21 degrees C+273.15). So, V₂ = 0.00654 L, T₂ = (57 degrees C+273.15).

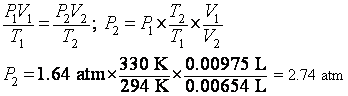
7.        What is the density of chlorine gas at STP?

STP means T = 273K and P = 1 atm. The density of a gas can be calculated from the IGL (Ideal Gas Law) since density is just mass per unit volume. If we take n, the number of moles, we can convert it to grams by using M, the molar mass: m = n´M which means . V is already in the IGL (PV = nRT), so we substitute for n:

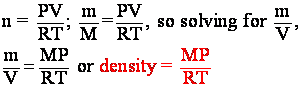
So now we have an expression for density in terms we know. If m is in grams and V is in liters, the density will be in g/L.

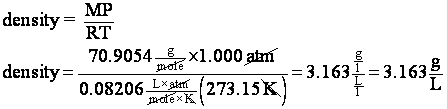
8.        What is the volume of 216.8 g of oxygen at STP?

STP means T = 273K and P = 1 atm. Since grams of oxygen are involved, it is clear that we have to use the IGL. We can use the 216.8 grams and the molar mass of oxygen to calculate n, the number of moles. STP gives us T and P. R is a constant that we know. So we're all set.

9.        What is the molar mass of a gas whose density is 1.96 g/L at STP?

From problem 7, we showed that . So, given the density and STP, we should be able to find M, the molar mass.

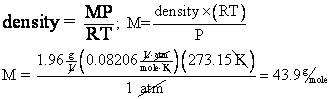
10.    What is the pressure of 2.50 moles of oxygen if the sample occupied 40.0 L at 25 degrees C?

Aha! The problem mentions moles! So we know it requires the use of the IGL. PV = nRT. Rearranging to give pressure,